Normalization

The normalization is especially to eliminate the following anomalies:
  Insertion anomaly
  Deletion anomaly
  Update anomaly
  Join anomaly

Goals of Normalization
   Integrity
   Maintainability

Side Effects of Normalization
  Reduced storage space required ( usually, but it could increase).
  Simpler queries ( Sometimes, but some could be more complex).
  Simpler updates ( sometimes, but some could be more complex).

First Normal From
  Relation should not contain any multi-valued, attribute.

Second Normal Form
  Relation R is in 2NF iff
     R should be in 1NF
     R should not contain any partial dependency.

Partial Dependency
  Let R be the relation schema and X,Y,A are non empty set of attributes.
  X : Any candidate key
  A : Non-prime attribute
  Y : Proper subset of any candidate key.

    Y→A is said to be partial dependency iff
      Y is proper subset of candidate key.
       A should be non-prime attribute.

Third Normal From
  Let R be the relation schema X→Y any non-trivial functional dependency over R is in 3NF iff
    R should be in 2NF
    X should be candidate key or super key, or
    Y should be prime attribute.

BCNF ( Boyce Codd Normal Form )
   Let R be relational schema X→Y be any non-trivial functional dependency over R is BCNF iff X is candidate key / Super Key.

4NF : Let R be the relational schema. F be the single and multivalued dependency X→→Y is in 4NF iff
   X : candidate key or super key or 
                  X ⋃ Y = R

Multivalued Dependency
    R be the relational schema x,y,z attribute sets over R and t1,t2,t3,t4 are tuples over R.
                         X→→Y only if
  1. t1.X = t2.X = t3.X = t4.X
  2.  t1.Y = t2.Y = t3.Y = t4.Y
  3.  t1.Z = t2.Z = t3.Z = t4.Z

complement Rule
   If  X → → Y
 then  X → → R - ( X ⋃ Y )
     X → → Z
 A multivalued dependency X → → Y is said to be trivial multivalued dependency:
          if  X⊇ Y  or  X⊎Y ≡ R
  Otherwise non-trivial multivalued dependency

 Equality of FD Set
     FD sets F and G are said to be equal iff
         (a) F covers G, and
         (b) G covers F

MINIMAL COVER OR CANONICAL COVER

    Minimal cover or canonical  cover is the one in which,
Every FD is simple ( RHS of any FD should have single attribute)
   Example: F = { A→BC }, here F = ( A→B , A→C} is simple.
        It is left reduced ( removal of extraneous symbols )
            Example: F = { AB→C , B→C}, here B is extraneous attribute.
               So F = { A→C, B→C}.
        It is non-redundant (eliminating unnecessary FDs)
           Example: F = { A→B , B→C , A→C }, here A→C is redundant,
               Hence, F = { A→B , B→C}.

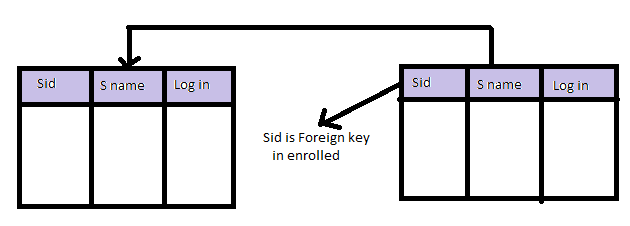
REFERENTIAL INTEGRITY CONSTRAINTS

   Foreign Key
      Foreign Key is a set of attributes that reference primary key or alternative key of the same relation or other relation.

  
Referenced Relation

 1. Insertion : no violation.
 2. Deletion:
     (a) On delete no action : Means if it causes problem on delete then not allowed to delete.
     (b) On delete cascade : If we want to delete primary key value from referenced table it will delete that value from referencing table also.
     (c) On delete set null : If we want to delete primary key from referenced table then it will try to set the null values in place of that value in referencing table.
3. Updation :
     (a) On update no action
     (b) On update cascade
     (c) On update set null

Referencing Relation
 Insertion: May cause violation
 Deletion: No violation 
 Updation: May cause violation

Example: 

  
             C is foreign key referencing A
       Delete ( 2,4 ) and on delete cascade.